Weird Behavior in the FiveThirtyEight 2020 Election Model

(This short post is just me writing down some of my thoughts after reading the analysis.)

Andrew Gelman wrote this very interesting analysis of the FiveThirtyEight(538) model in October — “Reverse-engineering the problematic tail behavior of the Fivethirtyeight presidential election forecast.” Three weeks after the election day, the 2020 election vote counts are almost finalized. We can see that the wider credible interval of the popular vote from the 538 model looks better on paper in hindsight (in contrast, for example, the economist’s model has a much narrower confidence interval). But is it justified? After all, everyone can tune their model to make uncertainty seems bigger, and explain the inaccuracy in their model with that artificially inflated uncertainly. (I’m not accusing 538 of doing so. I’m just saying that we shouldn’t blindly trust the computed uncertainty shown to us.)

One way to verify is to examine the results by state (or by county, if possible) and see if they are inside the 80% interval around 80% of the time. The problem is that errors in state forecasts are correlated, so this method wouldn’t work. One other way is to apply the model to all previous elections. But you then also need to account for some observed and unobserved trends in demographics and political circumstances (i.e., time becomes an important variable), so that also won’t be very reliable.

If it’s not easy to empirically prove the computed uncertainty, we can at least look at predictions given by the model and check if they comport with the data and our mental model to the world. Luckily, 538 made the simulation results (which I guess is from sampling some hierarchical Bayesian models?) public so we can all examine it.

Gelman spot some bizarre behavior in the 538 model, including inconsistent correlations in the tail, lack of correlation between states, and even negative correlation between states. The negative correlation between the results of Mississippi and Washington is one particular head-scratcher:

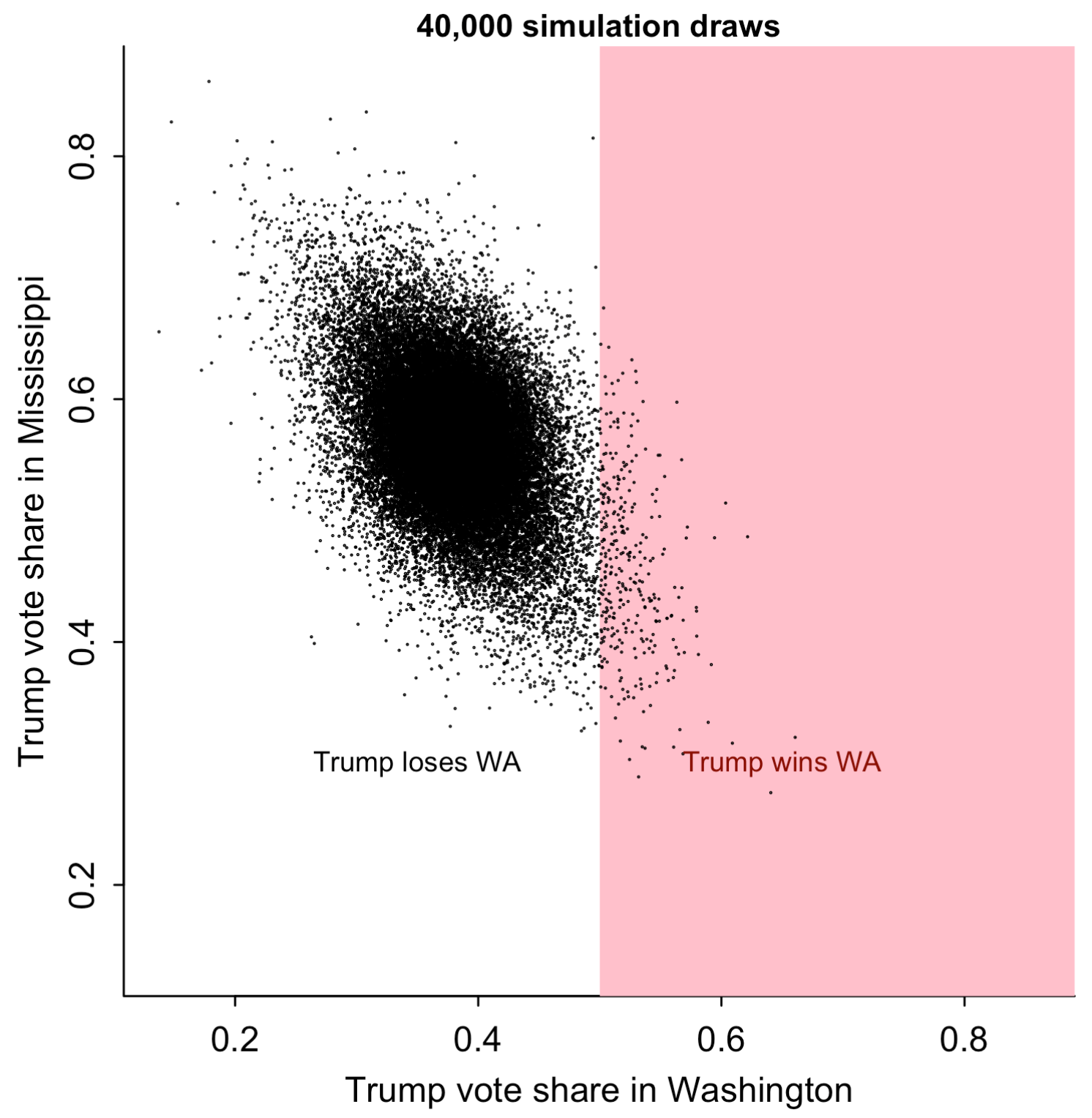
One possible reason for unintended negative correlations is accidentally using colliders(also, see Berkson’s paradox) in the model. Or it could simply be a bug in the code. I agree with Gelman that although polling errors could be negatively correlated, the confounding factors at the national level should have a much larger impact in extreme cases. You have to provide strong evidence to justify that negative correlation.

Divalent on the comment section of Gelman’s blog provided one possible explanation:

It would appear that this NJ/AK “error” is due not to the model trying to answer the Q “if Donald Trump, Republican, wins NJ, what is his odds of winning Alaska?”, but rather “What are the odds of the winner of NJ (whoever it might be) also winning Alaska?”

…

I suspect that if you look at presidential elections over the past 60 years, the winner of NJ was less likely to also win AK (and vice versa). So in a sense, that component would be “directionally correct”. (and given the output their model generates, they probably should reduce the weight of this particular component.

In my interpretation of this scenario, the collider is “the winner of NJ”. My causal diagram would be AK Votes -> AK Winner <- Party Affiliation -> NJ Winner <- NJ Votes (party affiliation is unknown here). The logic goes like — NJ winner tends to be a Democrat, and Democrat tends to lose AK, so they’ll likely to get fewer votes in AK. We shouldn’t condition on the winner of NJ and allow this flow of information from votes in NJ to votes in AK (as the AK votes should decide the AK winner, not the other way around). (The party affiliation also confounds the AK and NJ votes, but it doesn’t affect this analysis.)

Note that in this scenario, conditioning on the party affiliation will block the flow of information. If we know Donald Trump, a Republican, wins NJ, it doesn’t change the fact that he is also more favored to win AK. Any reasonable model should already have conditioned on party affiliation, so I’d say that this particular “component” does not exist. If it was accidentally added to the model, it should be removed completely, instead of reducing its weight.