Implementing Beam Search - Part 2
Advance Features that Regularize the Translator
Nov 7, 2018 · 1302 words · 7 minute read

Overview
Part one gave an overview on how OpenNMT-py produces output sequences for a batch of input sequences (Translator._translate_batch method), and how it conducts beam searches (Beam objects):
Implementing Beam Search (Part 1) - A Source Code Analysis of OpenNMT-py
Now we turn our attention to some of the details we skipped through in part one — the advanced features that influence how the translator produce output candidates/hypotheses. They can be put into two categories: rule-based and number-based.
More concretely, what these features aim to achieve includes:
-
Stipulate a minimum length of output candidates.
-
Prevent any n-grams from appearing more than once in the output (with exception of certain tokens).
-
Discourage or encourage longer output candidates.
-
Penalize when an output candidate references only a part of the input sequence.
-
Penalize when an output candidate repeats itself (focusing too much on the same part of the input sequence).
They can be used when the test corpus differs from the train corpus significantly, or when the model unfortunately was not able to learn the desired behaviors due to its limitations. They are essentially another set of hyper-parameters, but only relevant in test/inference stage.
Rule-based Regularizers
Minimum length of output candidates
This is controlled by the command line argument of translator.py: -min_length.
| cur_len = len(self.next_ys) | |
| if cur_len < self.min_length: | |
| for k in range(len(word_probs)): | |
| word_probs[k][self._eos] = -1e20 |
This is the second thing the Beam.advance method does after being called (The first thing is applying stepwise penalties, which will be covered later).
The logic is fairly simple: if we haven’t reached the desired minimum output lengths, then the probabilities of the EOS token being the next token should be set to very low (so the sequence won’t end here).
Block N-Gram Repeats
This is controlled by these command line arguments of translator.py: -block_ngram_repeat(the length of the N-gram, e.g. 1 means unigram) and -ignore_when_blocking(the N-gram should be ignored when it contains one of these tokens).
| if self.block_ngram_repeat > 0: | |
| ngrams = [] | |
| le = len(self.next_ys) | |
| for j in range(self.next_ys[-1].size(0)): | |
| hyp, _ = self.get_hyp(le - 1, j) | |
| ngrams = set() | |
| fail = False | |
| gram = [] | |
| for i in range(le - 1): | |
| # Last n tokens, n = block_ngram_repeat | |
| gram = (gram + | |
| [hyp[i].item()])[-self.block_ngram_repeat:] | |
| # Skip the blocking if it is in the exclusion list | |
| if set(gram) & self.exclusion_tokens: | |
| continue | |
| if tuple(gram) in ngrams: | |
| fail = True | |
| ngrams.add(tuple(gram)) | |
| if fail: | |
| beam_scores[j] = -10e20 |
This one is a bit more involved. The checking only happens when the Beam object already has at least one step worth of sequence predicted (len(self.prev_ks) > 0).
One interesting line is line 14. self.exclusion_tokens is a set that contains all the exception tokens, so the & operator here is not the regular logical AND operator, but a set intersection operator. It’ll return a set with non-zero size if any of the exception tokens appears in the list gram.
If any repetition occurs in the sequence so far, line 20 will set all next-token probabilities derived from that sequence to very low. This essentially prevents the last node of that sequence from expanding in the search tree.
Note that it does not prevent the sequence that contains repeated N-grams from being added to the search tree, but rather prevent those sequence from extending further. This can cause problems in some extreme cases and still lets the Beam object produce candidates that contains repeated N-grams, but it should be really rare if parameters are set properly.
Number-based Regularizers
These regularizers are managed by a GNMTGlobalScorer object, initialized in the function build_translator.
![X is the source; Y is the current target (source[1])](1*UT_C4eXxYK6cEhhZ1HIPig.png)
X is the source; Y is the current target (source[1])
Length normalization
This is controlled by these command line arguments of translator.py: -length_penalty (the following demonstrates the “wu” option[2]) and -alpha.
![|Y| is the current target length*; α* is the length normalization coefficient (source[1])](1*wbYSw6m118tFw5ovC4jV8A.png)
|Y| is the current target length*; α* is the length normalization coefficient (source[1])
Recall from part one that a probability of a sequence a_1, a_2, a_3can be calculated as a conditional probability P(a_1, a_2, a_3) = P(a_1)P(a_2|a_1)P(a_3|a_1, a_2). If we add a new token a_4 to this sequence, the probability of this new sequence is then P(a_1)P(a_2|a_1)P(a_3|a_1, a_2)P(a_4|a_1, a_2, a_3). We can see that the probability will only go exponentially lower as the sequence extends, especially when vocabulary is large and uncertainty is high.
We may want to slow the decay to a certain degree, hence the length normalization/penalty. The results of the lp function will be used to divide the log probability of the sequence. With 1> α > 0, the longer sequences are penalized less heavily when α is larger (i.e. longer sequences are more likely to be picked as the final output). (Log probabilities are negative numbers, so a log probability divided by a number > 1 will becomes larger.)
| def length_wu(self, beam, logprobs, alpha=0.): | |
| """ | |
| NMT length re-ranking score from | |
| "Google's Neural Machine Translation System" :cite:. | |
| """ | |
| modifier = (((5 + len(beam.next_ys)) ** alpha) / | |
| ((5 + 1) ** alpha)) | |
| return (logprobs / modifier) |
Theoretically α can be larger than 1 or less than 0, but I haven’t yet seen evidences that it’ll be beneficial to the results.
Coverage normalization
This is controlled by these command line arguments of translator.py: -coverage_penalty (two variations: “wu” and “summary”), -stepwise_penalty, and -beta.
The formula used in “wu” version[2]:
![pi,j is the attention probability of the j-th target word yj on the i-th source word *xi *(source[1])](1*EvpXElfNvVHyPo8_ZZRong.png)
pi,j is the attention probability of the j-th target word yj on the i-th source word *xi *(source[1])
The formula used in “summary” version:
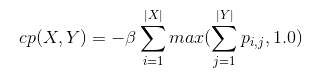
The β here are actually the -beta argument multiplied by -1.
The differences between these two formulae:
-
the log function in the first formula
-
Once the sum of p_ij over j reaches one, the penalty on position i in the source will become zero for formula 1.
-
The penalty will start to grow once the sum of p_ij over j reaches one for formula 2.
So we can see that formula 1 encourage the decoder to cover all time steps in the input; formula 2 on the other hand discourage the decoder of focusing too much on the same set of time steps in the input. Formula 1 is suitable for translation tasks; while formula 2 can be used for summarization tasks.
It can be really helpful if we calculate the penalty at every decoder time step when using the “summary” coverage normalization (formula 2), so the problematic sequence will be be extended further. That’s what stepwise_penalty does. You should set it to True when using this version of coverage normalization.
How are They Applied in Practice
The first thing Beam.advance method does is to apply coverage penalty if stepwise_penalty is set to True:
if self.stepwise_penalty:
self.global_scorer.update_score(self, attn_out)
| def update_score(self, beam, attn): | |
| """ | |
| Function to update scores of a Beam that is not finished | |
| """ | |
| if "prev_penalty" in beam.global_state.keys(): | |
| beam.scores.add_(beam.global_state["prev_penalty"]) | |
| penalty = self.cov_penalty(beam, | |
| beam.global_state["coverage"] + attn, | |
| self.beta) | |
| beam.scores.sub_(penalty) |
It removes the (coverage) penalty from the last time step, recalculate a new one, and then subtract it from the log probabilities.
Beam.advance invokes GNMTGlobalScorer.update_global_state method after it added a new set the new nodes to the search tree. The method keeps track of the sums of p_ij over j in beam.global_state['coverage'], and save the current coverage penalty for GNMTGlobalScorer.update_score to use later.
| def update_global_state(self, beam): | |
| "Keeps the coverage vector as sum of attentions" | |
| if len(beam.prev_ks) == 1: | |
| beam.global_state["prev_penalty"] = beam.scores.clone().fill_(0.0) | |
| beam.global_state["coverage"] = beam.attn[-1] | |
| self.cov_total = beam.attn[-1].sum(1) | |
| else: | |
| self.cov_total += torch.min(beam.attn[-1], | |
| beam.global_state['coverage']).sum(1) | |
| beam.global_state["coverage"] = beam.global_state["coverage"] \ | |
| .index_select(0, beam.prev_ks[-1]).add(beam.attn[-1]) | |
| prev_penalty = self.cov_penalty(beam, | |
| beam.global_state["coverage"], | |
| self.beta) | |
| beam.global_state["prev_penalty"] = prev_penalty |
(I failed to find the use of self.cov_total. It’s not used anywhere. You can safely ignore lines that includes it.) (The prev_penalty here is exactly the same as penalty in GNMTGlobalScorer.update_score.)
The length penalty is applied when a candidate is created (EOS appeared as a node):
| for i in range(self.next_ys[-1].size(0)): | |
| if self.next_ys[-1][i] == self._eos: | |
| global_scores = self.global_scorer.score(self, self.scores) | |
| s = global_scores[i] | |
| self.finished.append((s, len(self.next_ys) - 1, i)) |
| def score(self, beam, logprobs): | |
| """ | |
| Rescores a prediction based on penalty functions | |
| """ | |
| normalized_probs = self.length_penalty(beam, | |
| logprobs, | |
| self.alpha) | |
| if not beam.stepwise_penalty: | |
| penalty = self.cov_penalty(beam, | |
| beam.global_state["coverage"], | |
| self.beta) | |
| normalized_probs -= penalty | |
| return normalized_probs |
GNMTGlobalScorer.score only subtracts the coverage penalty from the scores when stepwise_penalty is False, as the penalty will have already been otherwise applied. (However, the results will be slightly different. When stepwise_penalty is True length penalty will be applied after coverage penalty; it’s the other way around when stepwise_penalty is not False.)
Fin
Thanks for reading! Writing this kind of code analysis is relative new to me, and I struggled a lot along the way. I’m very grateful that you find it bearable.
As we can see, the OpenNMT-py has some well modularized code in the part of the project. However, there are still some recalculations that can have been avoided, and some code that does not strictly follow the formula. None of them is a big problem, but you might want to take a note of them if you want to re-implement beam search yourself based on this.
There are a lot of details in this implementation. Unfortunately I did not find any tests in the OpenNMT-py projects that cover these part of the code. An interesting next step might be finding a package the does proper testing with beam search and learn from it.
References
-
Wu, Y., Schuster, M., Chen, Z., Le, Q. V, Norouzi, M., Macherey, W., … Dean, J. (2016). Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation.